23.02.24~ 23.03.02 동안 부트캠프에서 배웠던 내용을 정리한 학습일지입니다.
1주차는 하루하루에 대한 내용을 정리했는데 주차별 정리가 가능하다고 하여 작성 형식을 조금 변경했습니다 ㅎㅎ
(상관분석과 회귀분석의 경우 1주차에 내용과 겹쳐, 1주차 노션에 실습 내용을 추가했습니다)
기초통계 교육: https://solar-geology-c0d.notion.site/84eea31472cb481d80477757cc37ee7e
부트캠프 2주차 - 2023.02.24 ~ 2023.03.02 "기초통계 교육"
1. 통계학이란?
: 관심의 대상이 되는 집단(모집단)의 특성을 파악하기 위해 모집단으로부터 일부의 자료(표본)를 수집, 정리, 요약, 분석하여 표본의 특성을 파악하고 이를 이용하여 모집단의 특성에 대해 추론하는 원리와 방법을 배우는 학문.
- 통계학의 목적: 실무자의 주관적인 감, 추측에 의한 의사결정보다는 자료에 근거한 합리적 의사결정을 목표로 함
1.2 기초 통계
1.2.1 모집단과 표본
- 모집단: 아직 가지고 있지 않은 모르는 데이터를 포함한 모든 데이터 ; 관심의 대상이 되는 집합
- 표본: 모집단의 일부분에 해당되는 관측값들의 집합
- 모수: 모집단에 대한 요약치 ; 구하고 싶은 것
- 통계량: 표본에 대한 수치적 요약
- 확률변수: 확률 법칙에 따라 변화하는 값
- 확률분포: 확률변수와 그 값이 나올 수 있는 확률을 대응시켜 표시하는 것
1.2.2 변수와 도수
- 변수: 관심의 대상이 되는 특성 or 측정 결과
- 수치형 변수: 이산형 자료, 연속형 자료
- 범주형 변수: 명목형 자료, 순서형 자료
- 도수: 각 계급에 속하는 변량의 개수
- 계급: 변량을 일정한 간격으로 나눈 구간
- 계급을 정할 때 변량의 최소, 최대를 고려
- 상대도수: 각 계급에 속하는 변량의 비율
1.2.3 기초 통계량
- 모평균: 모집단의 평균
$$u = {\sum_{i=1}^N x_i \over N} $$
- 표본평균: 모평균의 추정값
$$\hat{u}=\; \bar{x} = {\sum_{i=1}^n x_i \over n} $$
- 중앙값: 주어진 값들을 크기의 순서대로 정렬했을 때, 가장 중앙에 위치하는 값
- Ⅰ) 데이터의 개수가 홀수 개일 때: ${n+1 \over 2}$ 번째 관측값
- Ⅱ) 데이터의 개수가 짝수 개일 때 : ${n \over 2}$, ${n+1 \over 2}$ 번째 관측값의 평균
- 모분산: 모집단의 분산 (데이터가 평균과 얼마나 떨어져 있는지 나타내는 지표) (엑셀에서 var.p)
$$ \sigma^2 = {1 \over N} \sum_{i=1}^{N}(x_{i}-u)^2 $$
- 표본분산: 모분산의 추정값 (엑셀에서 var.s)
$$ s^2 = {1 \over n-1} \sum_{i=1}^{n}(x_{i}-\bar{x})^2 $$
- 표준편차: 분산의 제곱근
$$ \sigma = \sqrt{{1 \over N} \sum_{i=1}^{N}(x_{i}-u)^2} $$
- 첨도: 데이터의 분포의 뾰족한 정도를 파악하는 지표 (첨도 = 3 : 정규분포, 첨도 > 3 : 납작한 분포, 첨도 < 3 : 뾰족한 분포)
- 왜도: 데이터 분포가 치우쳐 있는 정도를 나타내는 지표 (평균 = 중앙값: 왜도 = 0, 왜도 >0 : 오른쪽으로 꼬리가 긴 분포, 왜도 < 0 : 왼쪽으로 꼬리가 긴 분포)
💡 대표값으로서 평균과 중앙값
평균은 모든 데이터를 포함한 개념이지만 특이값에 취약하고 → not robust
중앙값은 모든 데이터를 포함하진 않지만 특이값에 강함 → robust
ex) 연봉
1.2.4 정규분포
: 통계학에서의 대표적인 연속 확률 분포

- 정규분포의 특징
- (-inf, inf)의 실수 값을 취함
- 중앙 부분이 평균이며, 평균을 기준으로 대칭
- 그래프가 종 모양을 가짐 ; 평균값 부근의 확률 밀도가 큼
- 표준편차의 값에 따라 정규 분포의 높낮이가 변함
- 정규분포의 중요성
- 많은 분야의 연속형 데이터들이 종모양 형태를 뜬다는 것이 확인
- 표본의 크기가 크다면, 중심극한 정리에 의해 모든 연속형 데이터는 표준정규분포를 따름
💡 중심극한 정리
평균이 $u$이고 분산이 $\sigma^2$ 인 모집단에서 임의 추출한 표본의 크기가 충분히 크면, 표본평균 $\bar{x}$ 은 근사적으로 정규분포 $N(u,\;{{\sigma^2} \over n})$을 따른다
$$ Z\; = \;{\bar{x} - u \over {\sigma \over \sqrt{n}} }\;\; \sim\;\; N(u,\;{{\sigma^2} \over n}) $$
- 표준화
- 다양한 형태의 정규분포를 표준 정규 분포로 변환하는 방법
- 중요성: 다양한 데이터를 균일한 기준으로 비교할 수 있음
$$ Z = {x - u \over \sigma } $$
2. 이상치 탐색
2.1 이상치란?
: 특정 지정된 그룹에 분 되지 못하는 값으로, 정상 군의 상한과 하한의 범위를 벗어나 있거나 패턴에 벗어난 수치
2.2 이상치 탐색
2.2.1 Z - Score
- Z-Score : 자료가 평균으로부터 표준편차의 몇 배만큼 떨어져 있는지를 나타내는 지표
$$ Z = {x - u \over \sigma } $$
- 특징
- Z > 0 : 자료 값이 평균보다 높음을 의미
- Z < 0: 자료 값이 평균보다 낮음을 의미
- Z ≈ 0 : 자료 값이 평균과 비슷함을 의미
- -3 ≤ Z ≤ 3 : 일반적으로 이상치로 판단하는 기준
2.2.2 사분위수
: 데이터를 4등분하는 값
- 제1 사분위수 (1Q) : ((N - 1) x 0.25) +1
- 제2 사분위수 (2Q) : 중앙값
- 제3 사분위수 (3Q) : ((N - 1 x 0.75) + 1
- IQR : 3Q - 1Q
- 이상치 범위
- 이상치 < 1Q - 1.5 IQR
- 3Q + 1.5 IQR > 이상치
2.2.3 Box Plot
: 5개의 수치적 자료를 활용해 데이터의 분포와 범위를 표현한 그래프로 데이터의 분포 파악, 이상치 존재 유무 확인 시 사용

3. 통계적 데이터 분석
3.1 가설과 유의확률
- 가설검정: 모수에 대한 가설이 적절한지 판단하는 방법
- 가설 종류
- 귀무가설 $H_{0}$ : 일반적으로 널리 인정되는 사실; 일반적 통념 or 기존의 방법
- 대립가설 $H_{1}$: 새롭게 주장하고자 하는 가설
- 유의확률 (P-Value)
- $H_{0}$가 맞다는 전제 하에, 표본에서 실제로 관측된 통계치와 같거나 더 극단적인 통계치가 관측될 확률
- 유의수준 $\alpha \; = 0.05$ 일 때, p-value값이 0.05보다 작을 경우 $H_{0}$ 기각 o
3.2 t-test
: 두 개 집단의 평균이 통계적으로 유의미한 차이가 있는지 검정하는 방법
- 시행 단계

- F-검정
- 두 집단의 등분산성을 검정
- $H_{0}$ : 두 집단의 분산은 같다 ($\sigma^2_{0} =\sigma^2_{1}$) $VS$ $H_{1}$: 두 집단의 분산은 다르다 ($\sigma^2_{0} \not= \sigma^2_{1}$)
- 수행법: [데이터] 탭 → 데이터 분석 → F-검정
- F- 검정 해석
- p-value < $\alpha$ 의 경우: $H_{0}$ 기각 o → 두 집단의 분산은 다르다 → 이분산 가정 t-test 진행
- p-value > $\alpha$ 의 경우: $H_{0}$ 기각 x → 두 집단의 분산은 동일하다 → 등분산 가정 t-test 진행
- t-test
- 두 집단의 평균이 유의미한 차이가 있는지 검정
- $H_{0}$ : 두 집단의 평균엔 유의미한 차이가 없다 ($u_{0} =u_{1}$) $VS$ $H_{1}$: 두 집단의 평균엔 유의미한 차이가 있다 ($u_{0} \not = u_{1}$)
- 수행법: [데이터] 탭 → 데이터 분석 → t-test (등분상 or 이분산)
- t-test 해석
- p-value < $\alpha$ 의 경우: $H_{0}$ 기각 o → 두 집단의 평균에 유의미한 차이가 있다
- p-value > $\alpha$ 의 경우: $H_{0}$ 기각 x → 두 집단의 평균엔 유의미한 차이가 없다
💡 t-test 해석 시 주의할 점
1) p-value 단측검정: $H_{0} : u_{0} > u_{1}$ $VS$ $H_{1}$: $not$ $H_{0}$ 형식의 가설일 때 보는 값
2) p-value 양측검정 : $H_{0}: u_{0} =u_{1} \;VS\; H_{1}: u_{0} \not=u_{1}$ 형식의 가설일 때 보는 값
3.3 시계열 데이터 분석
: 일정 기간에 대해 시간의 함수로 표현되는 데이터 ; 시간의 흐름에 따라 발생한 데이터
- 시계열 데이터 분석의 목표: 과거 시계열 데이터 특설 파악 및 미래 데이터 예측
- 시계열 데이터 분석 방법의 종류
- 정상 시계열: 규칙적인 패턴을 가진 시계열 데이터
- 비정상 시계열: 불규칙적인 패턴을 가진 데이터
- 대부분의 시계열 데이터의 경우 비정상 시계열
- 비정상 시계열의 경우 이해가 어렵기 때문에 정상 시계열로 변환하여 데이터 분석 수행

- 지수 평활법: 현재의 실제 값과 현재의 예측 값을 합산하여 미래의 예측 값을 구하는 방법
$$ F_{n+l} \; = \; \alpha \times Z_{n} \; + (1-\alpha) \times F_{n} $$
( $n$ : 현재 시점, $n+l$: 예측 시점, $\alpha$: 가중치 (0 < $\alpha$ < 1), $Z_{n}$: 실제값, $F_{n}$: 예측값 )

- 함수

1) Raw Data
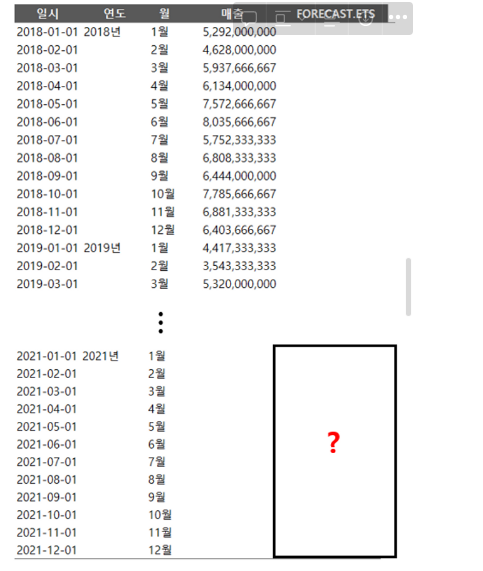
2) 목적
: 2018년 ~ 2020년의 월별 매출에 해당하는 데이터를 가지고 21년의 월별 매출 예측
3) 시계열 데이터 예측 진행

4) 결과
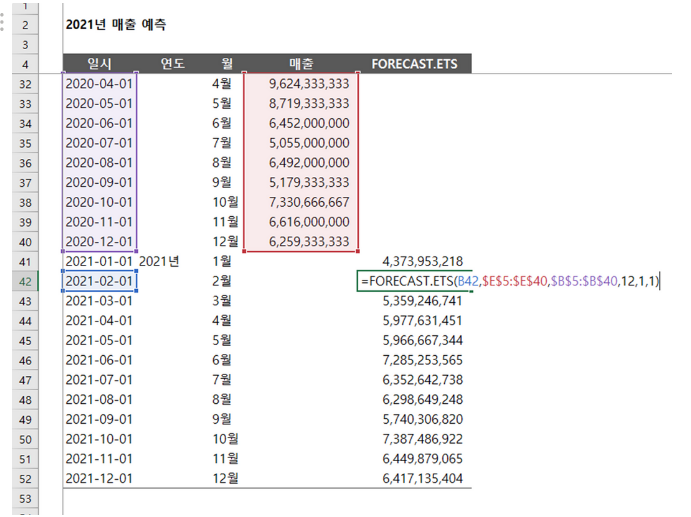
5) 그래프
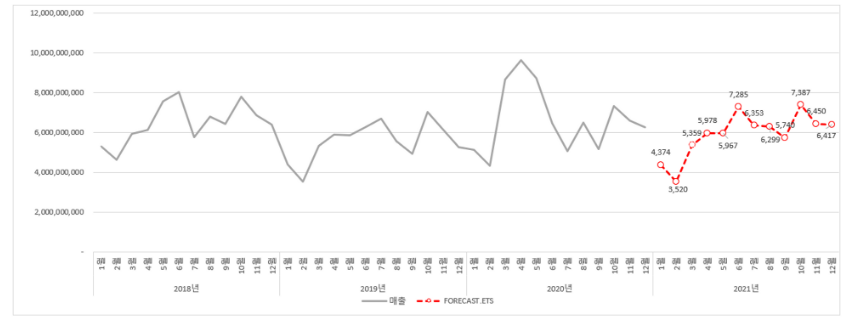
+ 2주차에는 기초 통계에 관한 내용을 수강했습니다.
개인적으로 2주차는 제가 통계학과라 수월하게 지나갔네요 ㅎㅎ
그래도 몇 개는 가물가물 했던 부분이 있었는데, 덕분에 개념을 다시 짚고 넘어갈 수 있는 시간이어서 좋았습니다 :)
그리고 처음으로 퀴즈를 봤습니다!
문제는 쉬웠는데 제가 문제를 잘못 읽어서 하나 틀린...핳
다음 퀴즈 때는 더 꼼꼼히 살펴보고 풀어야겠습니다.
'데이터 분석 > 데이터 분석 부트캠프' 카테고리의 다른 글
| [패스트캠퍼스] 데이터 분석 부트캠프 8기 5주차 학습일지 (0) | 2023.03.23 |
|---|---|
| [패스트캠퍼스] 데이터 분석 부트캠프 8기 4주차 학습일지 (0) | 2023.03.16 |
| [패스트캠퍼스] 데이터 분석 부트캠프 8기 3주차 학습일지 (0) | 2023.03.09 |
| [패스트캠퍼스] 데이터 분석 부트캠프 8기 1주차 학습일지 (0) | 2023.02.23 |
| [패스트캠퍼스] 데이터 분석 부트캠프 8기 합격 후기 (3) | 2023.02.20 |



