데이터 과학을 위한 통계를 바탕으로 작성되었습니다.
1. 임의표본추출과 표본편향
- 표본 (sample) : 더 큰 데이터 집합으로부터 얻은 부분집합
- 모집단 (population) : 어떤 데이터 집합을 구성하는 전체 집합
- 임의표본추출 (Random sampling) : 무작위로 표본을 추출하는 것
- 단순임의표본(simple random sample) : 층화 없이 임의표본추출로 얻은 표본
- 층화표본추출 (stratified sampling) : 모집단을 층으로 나눈 뒤, 각 층에서 무작위로 표본을 추출하는 것
- 계층(stratum) : 모집단의 공통된 특성을 가진 하위 그룹
- 표본편향 (sample tias) : 모집단을 잘못 대표하는 표본
2. 통계학에서의 표본분포
- 표본통계량 (sample statistic) : 모집단에서 추출된 표본으로부터 얻은 측정 지표 ex) 표본의 평균, 분포, 비율 등
- 데이터 분포 (data distribution) : 데이터 집합에서 각 개별 값의 도수분포
- 표본분포 (sampling distribution) : 하나의 동일한 모집단에서 얻은 여러 샘플들의 표본통계량 분포
- 중심극한정리 (central limit theorem) : 표본크기가 커질수록 표본분포가 정규분포를 따르는 경향.
→ 모집단이 정규분포가 아니더라도, 표본의 크기가 충분하고 데이터가 정규성을 따르는 경우, 여러 표본에서 추출한 평균은 정규분포에 근사
- 표준오차 (standard error) : 표본통계량의 변량. 표본분포의 변동성을 의미: $SE = {s \over \surd{n}} $
3. 부트스트랩
- 통계량이나 모수의 표본분포를 추정하는 쉽고 효과적인 방법
- 현재 있는 표본에서 추가적으로 표본을 복원추출하고, 각 표본에 대한 통계량과 모델을 다시 계산하는 것
- 데이터나 표본통계량이 정규분포를 따라야 한다는 전제가 필요 없음
[부트스트랩 알고리즘]

- 부트스트랩은 데이터의 크기가 작아서, 새로운 데이터를 만들기 위해 사용하는 기법이 아님
- 모집단에서 추가로 표본을 추출할때, 그 표본과 원래 표본이 비슷한지를 알려주는 개념
4. 신뢰구간
-신뢰구간: 알 수 없는 모수의 값이 포함될 가능성이 있는 값의 범위
- 신뢰수준: 같은 모집단으로부터 같은 방식으로 얻은 관심 통계량을 포함할 것으로 예상되는 신뢰구간의 백분율
5. 분포
5.1 정규분포
- 평균과 분산에 의해 모양이 결정되며, 평균을 중심으로 좌우 대칭을 보임

5.2 스튜던트 t 분포
- 정규분포와 유사하지만, 꼬리 부분이 더 두꺼운 형태
- t 분포에서 표본의 크기가 커질수록 정규분포에 근사
5.3 이항분포
- 각 시행마다 성공확률 p가 정해져 있을 때, 주어진 시행 횟수 n 중에서 성공한 횟수 x의 도수분포를 의미. $ X \sim\ B(n, p) $
- n이 충분히 큰 경우 이항분포는 정규분포에 근사(CLT)
5.4 카이제곱 분포
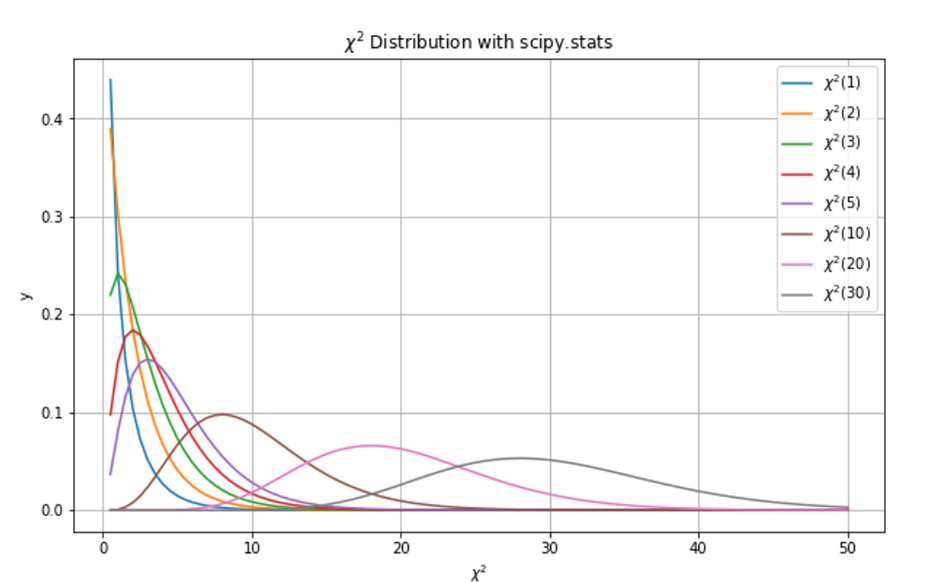
- k개의 서로 독립적인 표준정규분포를 따르는 확률변수를 각각 제곱한 다음 합해서 얻어지는 분포
- 이때 k를 자유도라 하며, 카이제곱 분포의 매개변수가 됨
- 카이제곱 통계량을 통해 여러 형태의 검정 진행
1) 적합도 검정: 관측 결과가 특정 분포를 따르는지
2) 동질성 검정: 두 집단의 분포가 동일한지
3) 독립성 검정: 두 변수 사이의 관계가 있는지
5.5 F 분포
- 독립적인 두 카이제곱분포에 관란 비로 정의
- 분산 분석, 회귀분석 등에 사용
'통계' 카테고리의 다른 글
| [통계] A/B Test (0) | 2023.07.10 |
|---|
