생존분석 수업을 듣고 진행한 백혈병 데이터 관련 분석입니다.
주제는 백혈병 환자의 골수이식 방법에 따른 비모수적, 모수적, 준모수적 접근 방법의 생존시간 비교입니다.
과거 분석한 내용을 다시 정리하는 거라 흐름이 조금 매끄럽지 않을수도 있고 의학 데이터를 처음 다뤄봐서 부족하지만 재미 삼아 봐주세요!
(사용한 데이터와 코드는 추후에 추가하겠습니다.)
1. 서론
백혈병이란 백혈구가 이상 증식하는 혈액종양의 일종으로, 제대로 성숙하지 못한 백혈구가 대량으로 혈액 속에 존재하는 것을 말한다. 백혈구의 비정상적인 증식에 비해 정상적인 혈구 세포의 수가 극히 적어지게 되면 면역기능 약화, 산소 운반, 영양 공급 등 기본적인 혈액의 기능을 수행할 수 없게 되는 문제가 발생한다. 백혈병 환자의 골수이식 종류는 크게 골수 공여자에 따라 동종이식과 자가이식 그리고 타인간이식 3가지로 구분되는데 본 분석에서는 자가 골수이식과 동종 골수이식 방법에 대해 초점을 두고 분석을 진행하였다.
자가 골수이식이란 자신의 좋은 골수만을 모았다가 사용하는 방법으로 자신의 골수를 넣기 때문에 이식거부반응이나 초기 합병증이 없는 장점이 있으나 치료율이 떨어지는 한계가 존재한다. 동종 골수이식이란 형제지간에 맞는 골수를 사용하는 것으로 가장 좋은 골수이식이라고 알려져 있으나 이식 후 이식거부 반응과 합병증이 뒤따를 수 있다는 문제점이 존재한다. 본 분석에서는 골수이식을 받은 백혈 병 환자들에 대해 골수이식 방법에 따른 생존시간을 비모수적, 모수적, 준모수적 접근 방법에 따라 비교 연구를 하고자 한다.
2. 연구 자료
2.1 연구 대상 및 자료
분석에 사용한 데이터는 국제 골수이식 협회에 보고된 최신 급성 골수성 백혈병을 가진 101명의 환자에 대한 데이터를 사용하였다. 데이터는 골수이식 방법에 따른 골수이식 후, 백혈병이 없는 생존기간을 월 단위로 기록한 데이터이다.
자가골수이식 그룹에 51명이 존재하며 이 중 중도절단된 케이스는 23명에 해당한다. 동종골수이식 그룹의 경우 50명이 해당하며 이 중 중도 절단된 경우는 28건이다. 변수는 다음과 같다.
· 변수 소개
- Survival times: 골수이식을 받은 후 생존기간
- Censored Observations: 중도절단 된 환자의 생존기간 (임의 우중도 절단)
분석에 사용 가능한 데이터로 만들기 위해 골수이식 방법 별(Autologous: 자가골수이식, Allogeneic: 동종골수이식) 생존기간과 중도 절단이 포함되어 있는 데이터이므로 중도 절단 여부(1: 중도 절단 발생 X 0: 중도 절단 발생 )로 필터링 작업을 수행하였다.
2.2 기초 자료 분석
다음은 골수이식 방법 별 기초 자료 분석이다. 중도절단 되지 않는 경우의 생존기간과 중도 절단된 데이터의 생존기간으로 분류하여 분석을 진행하였다. 여기서, 중도 절단된 데이터의 경우 연구가 종료되지 않아도 여러 이유로 더 이상 연구에 참여하지 못하는 임의 우중도 절단이다.

자가골수이식 방법의 경우 중도절단이 발생하지 않은 생존시간의 범위는 0.658(월)부터 56.086(월)이며,
중앙값은 7.434이다. 중도절단된 데이터의 경우 중앙값은 18.092(월)이다.

동종 골수 이식 방법의 경우 중도절단이 발생하지 않은 생존시간의 범위는 0.03(월)부터 20.066(월)이고
중앙값은 3.108이다. 중도절단된 경우의 중앙값은 28.717이다.

[그림 1]은 골수이식 방법 별 중도 절단이 발생하지 않은 생존시간의 히스토그램이다. 왼쪽이 자가골수이식, 오른쪽이 동종골수이식에 해당한다. 두 경우 모두 이식 초반에 백혈병이 발생하는 빈도가 높은 경우인 것을 알 수 있고, 동종 골수 이식의 경우가 초기 발병 케이스가 더 높은 것으로 보인다.

[그림 2]를 보면 중도 절단된 데이터의 경우 자가골수이식 방법의 경우 10-20구간에서 가장 많은 중도 절단이 발생하였고, 동종 골수 이식 방법의 경우 상대적으로 고르게 중도 절단이 발생했다는 것을 알 수 있다.
3. 비모수적, 모수적, 준모수적 접근 방법에 따른 골수이식 방법 별 생존시간 비교
3.1 비모수적 접근
가. Life - table
골수이식 방법 별 생존시간을 비교하기 위해 비모수적인 방법으로 접근하여 분석을 시행하였다. 비모수적 접근 방법의 대표적인 Life-table method를 사용하였으며 이는 주어진 데이터를 그룹 지어, 구간 시작점에서 생존 함수를 추정하는 방법이다. 측정 단위를 6개월의 일정한 폭으로 구분하여 분석을 진행하였다. 자가 골수 이식 방법의 경우 Life-table을 구해보면 다음과 같다.

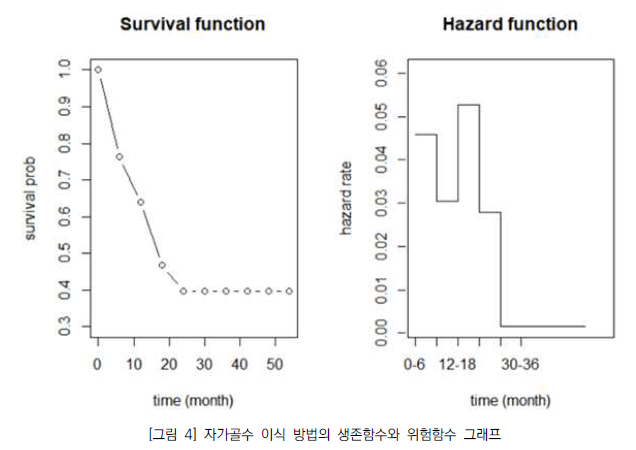
생존 함수는 t시간 이후에 사건이 발생할 확률. 즉, t시간까지 생존할 확률로 감소 함수이다. 위의 [그림 3]을 통해 생존 함수가 시간이 지날수록 감소하는 것을 알 수 있다. 또한 사망위험률이 가장 높은 구간은 위험 함숫값이 0.0518인 12-18(월)이다. 다음은 Life-table 분석을 이용한 결과를 가지고 생존 함수와 위험 함수의 그래프를 그린 것이다. 이를 통해 생존 함수가 시간이 흐를수록 감소하는 형태임을 쉽게 확인할 수 있다.
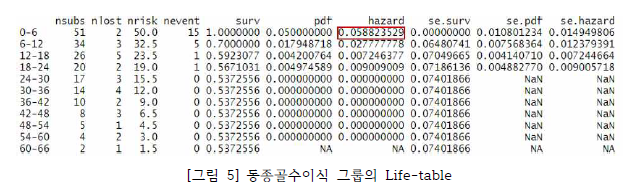
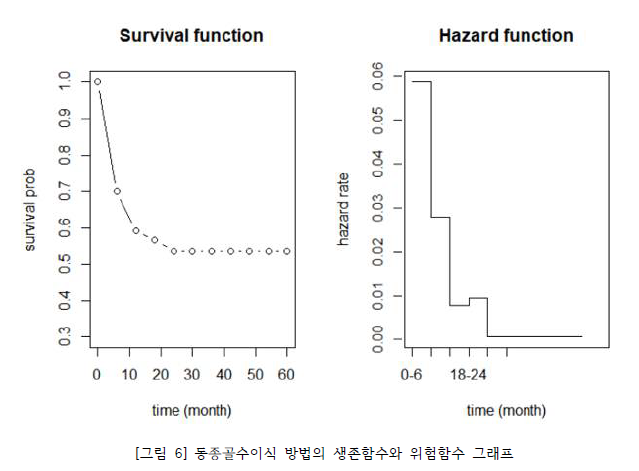
다음은 동종골수이식의 Life-table과 생존함수, 위험 함수의 그래프이다. [그림 5]를 통해 동종 골수이식의 경우 사망 위험률이 가장 높은 구간은 0.0588로 0-6(월)인 것을 확인할 수 있다. 자가골수이식 방법과 비교했을 때 상대적으로 초기 위험률이 높은 것으로 보이는데, 이를 확실하게 하기 위해서는 데이터의 분포 형태가 다름으로 추가적인 분석이 필요하다.
나. Kaplan-Meier 추정량을 이용한 생존함수의 비교
앞서 분석한 Life-table method 결과로 두 그룹의 위험률의 형태가 다르다는 것을 확인하였으나, [그림 1]과 [그림 2]에서 확인할 수 있듯 두 그룹의 분포 형태와 중도 절단 형태가 다름으로 Life-table 분석 결과를 확실시하기는 어렵다. 그러므로 두 그룹의 생존 함수 동일성 여부 검정하기 위해 추가적으로 Kaplan-Meier 추정량을 이용하여 로그-순위 검정과 가중 로그- 순위 검정을 진행하였다.
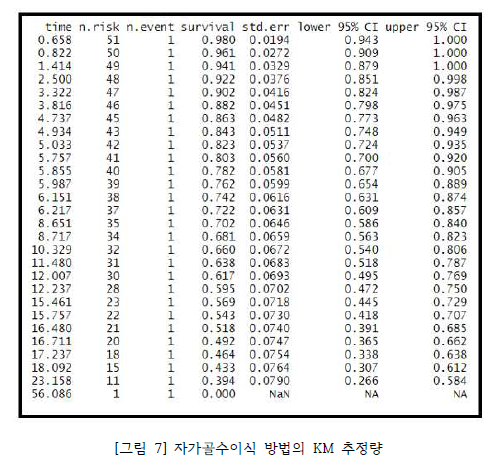
여기서 Kaplan-Meier 추정량이란 사건이 발생한 시점마다 구간 생존율을 구하여 이들의 누적으로 누적 생존율을 추정하는 방법을 말한다. 중도절단 자료가 포함되어 있는 경우 kaplan-Meier 추정량을 구하는 방법은 다음과 같은 방식으로 계산되고 [그림 7], [그림 8]이 이에 해당한다.

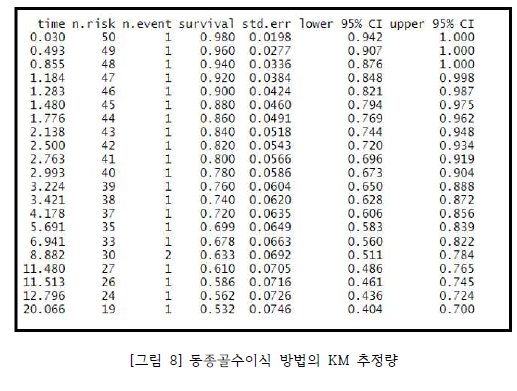
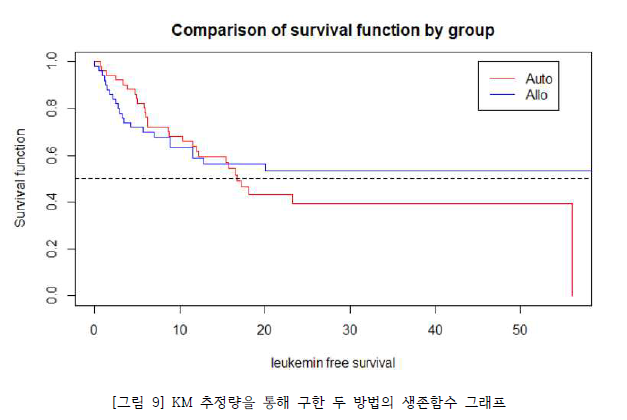
[그림 9]는 두 그룹의 생존함수 그린 그래프이다. 그래프에 표시된 점선의 경우 중간 수명을 표시한 것이다. 그래프를 보면, 초기에는 동종골수이식에 비해 자가골수이식 방법의 생존 함숫값이 더 높은 형태를, 시간이 흐를수록 동종골수이식의 생존 함숫값이 자가골수이식의 경우보다 더 높아지는 것을 확인할 수 있다. 또한 중간 수명의 경우 동종골수 이식이 자가골수이식 방법보다 더 높은 것일 확인할 수 있다. [그림 9]를 통해 두 그룹의 생존 함수의 형태가 차이가 있다는 것을 확인하였으나, 이 차이가 유의미한 차이인지 확인하기 위하여 로그-순위 검정과 가중 로그-순위 검정을 실행하였다. 로그-순위 검정과 가중 로그-순위 검정에 사용된 귀무가설과 대립 가설은 다음과 같다.


로그-순위 검정 결과, 검정통계량 값이 0.4이고 유의수준 0.1%에서 검정 시, p-value가 0.5로 귀무가설을 기각하지 못한다.
즉, 두 그룹의 생존 함수는 차이가 없다는 것을 알 수 있다.
이를 확실시하기 위해 시간대마다 가중치를 다르게 주는 가중 로그-순위 검정을 시행하였다.

[그림 9]를 통해 두 그룹의 생존함수가 초기와 후반부에 형태가 달라지는 것을 확인할 수 있다. 이 차이가 유의미한 차이인지 확인하기 위해 초반부에 가중치를 주는 (rho = 1) 가중 로그-순위 검정 결과는 검정통계량 값이 0이고 유의확률이 1로, 유의순준 0.1%에서 검정 시 귀무가설을 기각하지 못한다. 그러므로 두 그룹의 생존 함수가 동일하다는 것을 알 수 있다.

[그림 12]는 생존함수의 후반부에 가중치를 주는(rho = -1) 가중 로그-순위 검정 결과이다. 검정 결과 검정통계량이 1.5, 유의확률이 0.2로 두 그룹의 생존 함수에 차이가 없다는 것을 알 수 있다.
3.2 모수적 접근
골수이식 방법 별 생존시간을 비교하기 위해 모수적인 방법으로 접근하여 분석을 진행하였다.
모수분포가 지수 분포, 와이블 분포, 로그 로지스틱, 로그 정규분포를 따른다고 가정하고 분석을 진행하였으며 최적의 모형을 선택하기 위한 기준으로 AIC를 사용하였다.
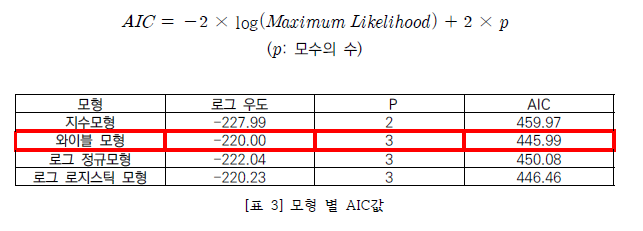
[표 3]은 모형에 따른 로그 우도값, 모수의 수, AIC 값을 정리해둔 표이다. [표 3]에서 확인할 수 있듯 AIC 값을 기준으로 했을 때 가장 작은 값을 가진 경우가 최적의 모형임으로 모수의 분포가 와이블 모형인 경우가 선택되었고 분석의 결과는 [그림 13]에 해당한다. 추정된 생존 함수는 $logT = 3.595 + 0.347 \times I(Method = 2) + \sigma^{2}_{\epsilon_{i}} $이다.
골수 이식 방법에 따른 생존함수를 구해보면 다음과 같다.
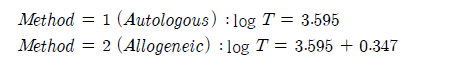
회귀계수에 대한 유의성 검정에 사용되는 가설은 다음과 같다.
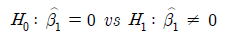
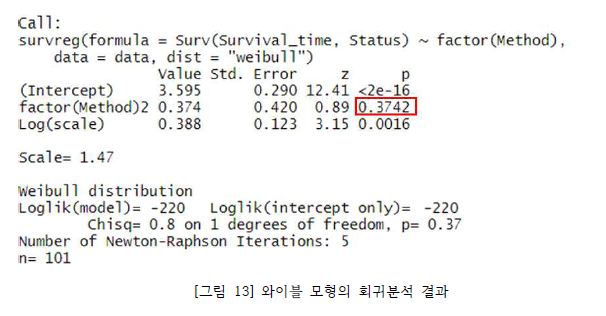
유의수준이 0.1일 때 ‘method’ 변수에 대한 유의성 검정 결과 변수의 유의확률이 0.3742로 유의하지 않다는 것을 확인할 수 있다. 해당 모형의 경우 공변량이 하나인 모형이기 때문에 ‘method’가 유의하지 않음으로 두 그룹의 생존 함수에 큰 차이가 없다는 것으로 생각할 수 있다. 모형이 유의하지 않아도 공변량의 효과에 대해 보면, $ \hat{\sigma} = \frac{1}{\alpha} = \frac{1}{1.47}$이며, 골수이식 방법에 따른 공변량의 효과는 $\hat{\beta} \times \hat{\alpha} = 0.25$이다. 추가로 추정된 생존 함수를 통해 두 그룹의 생존 함수를 비교하면 $\hat{\beta}$ 값이 0.347로 0보다 크기 때문에 $S_{1}(t) < S_{2}(t) $의 관계를 도출할 수 있다.
3.3 준모수적 접근
골수이식 방법 별 생존시간을 비교하기 위해 마지막으로 준모수적인 방법으로 접근하여 분석을 진행하였다.
분석에는 Cox’s의 비례위험모형이 사용되었다.

[그림 14]를 보면 골수이식 방법에 대한 회귀계수의 유의확률은 0.539로 유의수준 0.1%에서 검정 시, 귀무가설이 기각되어 추정된 모수가 유의하지 않다고 할 수 있다. 그러므로 두 그룹의 생존 함수 또한 큰 차이를 가지지 않을 것으로 보인다. Cox’s의 비례위험모형의 경우도 모형이 유의하지는 않지만 위험비에 대해 생각해 보면 그룹 2의 위험 함수는 그룹 1의 위험 함수의 0.84배라는 것을 알 수 있다
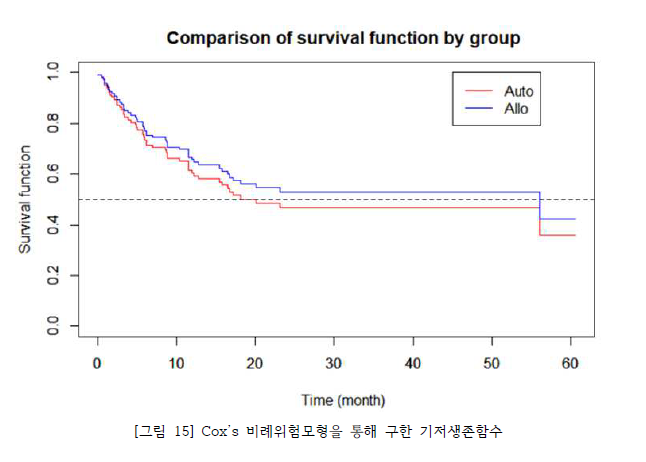
[그림 15]는 Cox’s의 비례위험 모형을 통해 구한 기저생존함수이다. [그림 9]와 비교했을 때, 생존 함수의 형태에 차이는 있지만 분석의 결과들을 조합해 보면 유의미한 차이는 아닌 것으로 보인다.
4. 결론
본 연구는 백혈병 환자의 골수이식 방법에 따른 생존시간의 차이를 비교하고자 수행되었다. 이를 위해 국제골수이식협회에 보고된 최신 급성 골수성 백혈병 자료를 사용하여 분석하였으며, 본 데이터에는 임의 우중도 절단 데이터가 포함되어 있다.
비모수적 접근으로 Life-table과 KM방법을 이용하였다. Life-table을 통해 자가골수이식과 동종골수이식 방법의 위험률 함수를 비교해본 결과 후자의 경우는 초기 위험률이 높은 형태, 전자의 경우 상대적으로 시간이 조금 흐른 후의 위험률이 높은 것을 확인하였다. 또한 KM방법을 통해 두 골수이식 방법의 생존 함수를 추정하고 로그-순위 검정과 가중 로그-순위 검정을 실시한 결과 두 그룹의 생존함수는 유의미한 차이는 존재하지 않다는 것을 알 수 있었다.
모수적 접근방법에서는 와이블 분포 가정을 하는 경우 AIC값이 가장 낮았지만 분석 결과 골수 이식 방법에 따른 유의미한 차이는 없다는 것을 확인하였고, 준모수적 접근 방법인 Cox’s의 비례위험모형에서도 골수이식 방법에 따른 공변량의 효과는 유의하지 않는 것으로 나타났다. 이를 정리하면 비모수적, 모수적, 준모수적 접근을 통해 두 그룹의 생존 함수를 추정한 결과 모두 동일하게 두 그룹의 생존함수에는 차이가 없는 것으로 나타났기 때문에 골수이식 방법에 따른 생존시간의 차이는 크지 않다는 것을 알 수 있다. 다만 중도 절단 데이터의 분포의 경우가 다르고 데이터의 크기가 작기 때문에 이 문제가 보안된다면 다른 결과를 도출할 수 있을 것으로 보인다.
'데이터 분석 > 프로젝트' 카테고리의 다른 글
| [Python] 유통 데이터를 활용한 리텐션과 RFM 분석(1) (0) | 2024.07.21 |
|---|---|
| [마케팅 데이터 분석] AARRR 실습(1) - Acquisition (2) | 2023.09.09 |
| [논문] Encoder Decoder 알고리즘을 이용한 시계열 자료 예측 (1) | 2022.08.11 |
| 위드(with)코로나 시대 소비 변화 - 번외 (0) | 2022.08.09 |
| 위드(with)코로나 시대 소비 변화 (0) | 2022.08.09 |



